いろいろやりたい

プロフィール

ＨＮ：

turkey

年齢：

性別：

男性

誕生日：

1993/11/30

職業：

学生

趣味：

プログラミング/電子工作

04.30.00:42

[PR]

[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。

04/30/00:42

06.21.14:13

電子回路のお勉強その１ウィーンブリッジ発振回路理論編

さて、理論編です。
前回のとおりこのウィーンブリッジ発振回路は２つのパートからなると書きました。
まずは発振回路の仕組みからですかね。この辺は自分もさっぱりなので感覚だけでもつかめればいいと思っています。

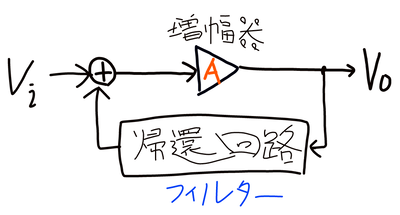
この回路において定義をします。
${\color{Gray} A }$ ：増幅率何倍に増幅するかを表す。もちろん増幅器で増幅される
${\color{Gray} \beta }$ ：帰還率　帰還回路で何倍の値を帰還させるか

例えば増幅率 ${\color{Gray} A }$ が3（３倍に増幅）で帰還率 ${\color{Gray} \beta }$ が 0.5（増幅した信号の半分を帰還）として最初の入力を１として考えましょう。
１　→　増幅(1*3) = 3　→　帰還(3*0.5) = 1.5　→　増幅(1.5 * 3) = 4.5　→
　　　　　　　　　　　　　　　　　　→　帰還(4.5 * 0.5) = 2.25　→　増幅(2.25 * 3) = 6.75 ......
というようにだんだんと大きくなっていき飽和します。
つまり
　 ${\color{Gray} A \times \beta > 1}$ 　：　飽和
　 ${\color{Gray} A \times \beta < 1}$ 　：　減衰
ということが分かります。

では
　 ${\color{Gray} A \times \beta = 1}$
のときはどうなるか

増幅率 ${\color{Gray} A }$ が4で帰還率 ${\color{Gray} \beta }$ が 0.25で考えてみましょう
１　→　増幅(1*4) = 4　→　帰還(4*0.25) = 1　→　増幅(1*4) = 4　→
　　　　　　　　　　　　　　　　　　→　帰還(4 * 0.25) = 1　......
同じ信号を永遠と繰り返すことが出ます。
つまりこれが発振です。

同じ信号といいましたがこれは帰還回路で決めることができます。帰還回路がフィルターになるわけです。
また入力信号と同位相のものを帰還させることを正帰還、逆位相のものを帰還させることを負帰還といいます。ウィーンブリッジ発振回路では正帰還を使います。

では実際の回路と見比べながらどこが増幅器で、どこが帰還回路に該当するか見てみましょう。

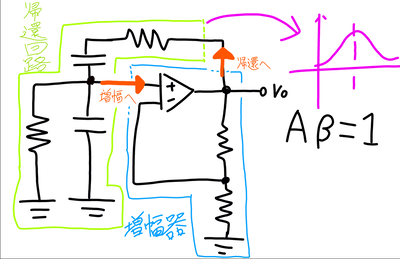
このように増幅した信号を帰還しています。
前回の例では増幅率 3、帰還率 1/3でやっていました。
もちろん増幅率、帰還率は部品定数によって決まるので求めてみましょう。

１．増幅率を求める
まずは増幅率です。
この増幅器は非反転増幅回路というものでそこだけ取り出すと次のような回路です。

それでは求めていきましょう。
オペアンプの特性から次の式が成り立ちます。
ここでの ${\color{Gray}\alpha}$ は電圧増幅度といい（Ａとは別物）、それぞれのオペアンプに固有の値をとります。電圧増幅度はデータシートに値も載っていますが、ここでは理想オペアンプとして計算しています。
　 ${\color{Gray} Vout = A\{(Vin+)\: + \: (Vin-)\}}$
（１式）

R1、R2で分圧しているので次の式も成り立ちます。
　 ${\color{Gray} Vin- = \frac{R_{3}}{R_{3} \: + \: R_{4}}Vout}$
（２式）

回路図から
　 ${\color{Gray} Vo = Vout}$
　 ${\color{Gray} Vin+ = Vi}$
となっているので（１式）、（２式）は
　 ${\color{Gray} Vo = \alpha(Vo \: - \:Vin-)}$
　 ${\color{Gray} Vin- = \frac{R_{3}}{R_{3} \: + \: R_{4}}Vo}$
となります。（１式）へ（２式）を代入すると
　 ${\color{Gray} Vo = \alpha(Vi \: - \: \frac{R_{3}}{R_{3}\:+\:R_{4}}Vo)}$
これを変形していきます
　 ${\color{Gray} Vo = \alpha*Vi \: - \: \frac{\alpha*R_{3}}{R_{3}\:+\:R_{4}}Vo}$
　 ${\color{Gray} Vo(1\:+\:\frac{\alpha*R_{3}}{R_{3}\:+\:R_{4}}) = \alpha*Vi}$
　 ${\color{Gray} Vo = \frac{\alpha*Vi}{1\:+\:\frac{\alpha*R_{3}}{R_{3}\:+\:R_{4}}}}$
　 ${\color{Gray} = \frac{\alpha*Vi(R_{3}\:+\:R_{4})}{(R_{3}\:+\:R_{4})\:+\:\alpha*R_{3}}}$
　 ${\color{Gray} = \frac{Vi(R_{3}\:+\:R_{4})}{\frac{R_{3}\:+\:R_{4}}{\alpha}\:+\:R_{3}}}$
オペアンプの理想として ${\color{Gray}\alpha}$ は無限大なので
　 ${\color{Gray} Vo = \lim_{\alpha\rightarrow \infty }\frac{Vi(R_{3}\:+\:R_{4})}{\frac{R_{3}\:+\:R_{4}}{\alpha}\:+\:R_{3}}}$
　 ${\color{Gray} Vo = \frac{(R_{3} \: + \:R_{4})}{R_{3}}Vi}$
　
こうしてやっと増幅度Ａが求まります。ViがVoに増幅されているわけですから
　 ${\color{Red}A=\frac{R_{3}\:+\:R_{4}}{R_{3}}}$
　 ${\color{Red}=1\:+\:\frac{R_{4}}{R_{3}}}$
　（式３）

R1とR2はもちろん正の数なのでＡは必ず１以上となることもわかります。

２．帰還率を求める
前回の回路図から帰還回路のみ取り出すと

緑の部分は

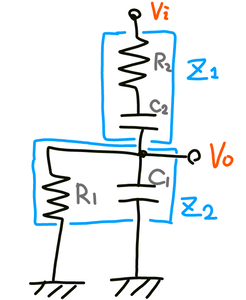
これが帰還回路であり、Viから入ってきた信号の帰還率だけVoへとだすものです。
まず青い枠で囲ったようにZ1とZ2のインピーダンスを求めます。
　 ${\color{Gray} Z_{1} = R_{2} \: + \: (\frac{1}{j\omega C_{2}})}$
　 ${\color{Gray} Z_{2} = \frac{R_{1} \times \frac{1}{j\omega C_{1}}}{R_{1} \: + \:\frac{1}{j\omega C_{1}}}}$
　
VoはZ1、Z2でViを分圧したものだから
　 ${\color{Gray} Vo = \frac{Z_{2}}{Z_{1}\:+\:Z_{2}}Vi}$
帰還率βは
　 ${\color{Gray} \beta = \frac{Vo}{Vi} = \frac{Z_{2}}{Z_{1}\:+\:Z_{2}}}$

発振する条件は
　 ${\color{Red} A \times \beta = 1}$
だったのでそれぞれ代入すると
　 ${\color{Gray} 1 = \frac{R_{3}\:+\:R_{4}}{R_{3}}\times\frac{Z_{2}}{Z_{1}\:+\:Z_{2}}}$
　 ${\color{Gray} \frac{Z_{1}\:+\:Z_{2}}{Z_{2}} = \frac{R_{3}\:+\:R_{4}}{R_{3}}}$ （式４）

（式４の左辺）について
　 ${\color{Gray} \frac{Z_{1}\:+\:Z_{2}}{Z_{2}} = \frac{(\frac{R_{1}\times\frac{1}{j \omega C_{1}}}{R_{1} \: + \: \frac{1}{j \omega C_{1}}})\:+\:(R_{2} + \frac{1}{j \omega C_{2}})}{(\frac{R_{1}\times\frac{1}{j \omega C_{1}}}{R_{1} \: + \: \frac{1}{j \omega C_{1}}})}}$
　 ${\color{Gray} = \frac{(\frac{R_{1}}{j \omega C_{1}R_{1} \: + \: 1})\:+\:(R_{2} + \frac{1}{j \omega C_{2}})}{\frac{R_{1}}{j \omega C_{1}R_{1} \: + \: 1}}}$
分子分母にjωC2をかけて
　 ${\color{Gray} = \frac{(\frac{j \omega C_{2}R_{1}}{j \omega C_{1}R_{1} \: + \: 1})\:+\:(j \omega C_{2}R_{2} + 1)}{\frac{j \omega C_{2}R_{1}}{j \omega C_{1}R_{1} \: + \: 1}}}$
分母分子にjωC1R1＋1をかけて
　 ${\color{Gray}= \frac{(jwC_{2}R_{1}) + (jwC_{2}R_{2}+1)(jwC_{1}R_{1} + 1)}{jwC_{2}R_{1}} }$
分子の展開をして
　 ${\color{Gray} = \frac{(j \omega C_{2}R_{1})+ (-\omega^2C_{1}C_{2}R_{1}R_{2})+(j \omega C_{2}R_{2})+ (j \omega C_{1}R_{1})}{j \omega C_{2}R_{1}}}$
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ${\color{Gray} + \frac{(j \omega C_{1}R_{1}+1)}{j \omega C_{2}R_{1}}}$
　 ${\color{Gray} = 1\:+\:\frac{1\:-\:\omega^2 C_{1}C_{2}R_{1}R_{2}}{j \omega C_{2}R_{1}}\:+\:\frac{R_{2}}{R_{1}}\:+\:\frac{C_{1}}{C_{2}}}$
　 ${\color{Gray} = 1\:+\:\frac{R_{2}}{R_{1}}\:+\:\frac{C_{1}}{C_{2}}\:-j(\frac{1\:-\:\omega^2 C_{1}C_{2}R_{1}R_{2}}{\omega C_{2}R_{1}})}$

（式４）へ代入すると
　 ${\color{Gray} \frac{R_{3}+R_{4}}{R_{4}} = 1\:+\:\frac{R_{2}}{R_{1}}\:+\:\frac{C_{1}}{C_{2}}\:-j(\frac{1\:-\:\omega^2 C_{1}C_{2}R_{1}R_{2}}{\omega C_{2}R_{1}})}$

両辺がイコールとして成立するには左辺が実数なので右辺も実数でないといけません。よって虚部は０です。
また別の考え方として左辺は帰還するときの信号を表す式に使われていたので、増幅された信号（実数→位相０）と位相が同じでないといけない、つまり位相０でないといけないので虚部は０です。
実際０になるのは正弦波のみです。普通の信号、つまりいろんな周波数の混ざった信号の場合、信号が同位相の周波数成分（虚部が０に近くなるような値）のみ増幅される結果となります。これは虚部がω以外すべて定数で虚部はωによって決まるからです。
信号は多種多様な正弦波から足し合わせてできていると考えることができるのである周波数だけの信号を取り出すことで正弦波が出力されます。

${\color{Green} \frac{R_{3}+R_{4}}{R_{4}} = 1\:+\:\frac{R_{2}}{R_{1}}\:+\:\frac{C_{1}}{C_{2}}}$ （発振条件その１）

虚部は０でないといけないという条件から
　 ${\color{Gray} \frac{1 \: - \: \omega^2C_{1}C_{2}R_{1}R_{2}}{\omega C_{2}R_{1}} = 0}$
　 ${\color{Gray} 1 \:-\:\omega^2C_{1}C_{2}R_{1}R_{2} = 0}$
よって
　 ${\color{Gray} \omega = \frac{1}{\sqrt{C_{1}C_{2}R_{1}R_{2}}}}$
ω＝２πｆより
　 ${\color{Green} f = \frac{1}{2\pi\sqrt{C_{1}C_{2}R_{1}R_{2}}}}$ （発振条件その２）

すごく長くなってしまいましたが、この２つの条件がそろうとき発振が起こります。
なので部品定数は出力したい周波数をきめればもとめることができます。

<参考文献>
・アナログ回路の基礎
・ウィーンブリッジ発振回路の動作原理
・オペアンプの基礎と応用　

無題

式4の左辺の展開式
「分子の展開をして」の直後の展開式が間違っています。

(jωC1R1)という項は出てきません。